I’ve been doing a bit of Leetcode to prepare for interviews. It’s kind of the bane of my existence but I believe it does prepare me well for interviews and I feel more confident in the language when I know I can solve a bunch of problems using it.

This is a really interesting problem I came across: Leetcode #37: Sudoku Solver

I like it because it feels a lot more creative than the other problems on the site. It doesn’t seem like there’s a time constraint on solutions either, which is nice because my solution is not optimized at ALL.

I spent 2 days trying to solve this, and when I finally got a solution I was beyond happy. So let’s look at what it takes to make a Sudoku solver.

If you’re interested in making your own solver, I highly recommend trying out the Leetcode problem first. There are definitely multiple ways to solve this, and you’ll find that the problem is simpler than it first seems, and then you’ll find that it’s slightly more complex than you thought. Nonetheless, it’s very rewarding when the solver finally works.

The rules of the game

Sudoku consists of a 9x9 grid that must be filled with the numbers 1,2,…,9. There are 3 sets of rules:

Each of the digits 1-9 must occur exactly once in each row.
Each of the digits 1-9 must occur exactly once in each column.
Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

These rules overlap, so for each cell we are always trying to satisfy all 3 criteria.

The approach

Take a look again at the grid. What steps would you take to solve it?

One approach could be to go through each number, locating all pre-existing occurrences of it. Each number has a “region of influence” that prevents a duplicate of it from being placed in its row/column/box, so by looking at cells outside the region of influence you can deduce where the number should be.

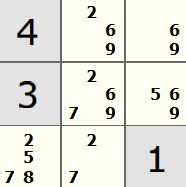
Another approach could be to look at each cell and see what potential candidates can exist in this cell. This is similar to the “penciling-in” approach (shown above) one might do when solving Sudoku by hand. This is the strategy I followed to make the solver.

Step 1: Creating the list of candidates

We need to iterate through every cell in the board once to generate a lsit of candidates. First, we ininitialize the candidates list, which is a 9x9 grid where each element corresponds to a set of possibilities. We initialize each set to contain the number -1 alone.

candidates = [[set([-1])]*9 for i in range(9)]

Then, we iterate through every cell in the board. In the problem, "." represents empty cells.

for i in range(len(board)):
    for j in range(len(board[0])):
        curr = board[i][j]
        if curr != ".":
            candidates[i][j] = set([-1])
            continue

So now, our corresponding cell lives at the (i,j) i.e. (y,x) coordinate. At this cell, we iterate through numbers 1-9, checking if the cell’s row/column/box contain that number. If it does contain the number, then we certainly can’t add our own number there since that is within the region of influence of the older number.

    curr_set = set()
    for n in range(1,10):
        if self.is_x_in_row(i,n,board) or \
           self.is_x_in_col(j,n,board) or \
           self.is_x_in_box(j // 3, i // 3, n,board):
            continue
        else:
            curr_set.add(n)
    if len(curr_set) == 0: # indicates invalid position
        # print("oops")
        return (False, board)
    candidates[i][j] = curr_set

The helper functions is_x_in_row(), is_x_in_col(), and is_x_in_box() do what they’re called – they extract the row/col/box given a coordinate, and check if n is within that.

After iterating through the entire board, we’ve created candidates. Next, we use the sets we created here to solve the puzzle.

Step 2: Using the candidate list

Given these candidates, our next step is to look for numbers that can ONLY exist in one cell in their row/col/box. For example, if in Row 1, the number “1” can only occur in the leftmost cell, then we know “1” must go there, regardless of its possibilities in the cell’s column or box. This is because the rules require each digit to occur once in each row/col/box. So, for a given number n, we must place it in the cell if either:

This is the only place n can be in the entire row
This is the only place n can be in the entire column
This is the only plane n can be in the entire box
n is the only possible number in this cell

So how do we do that? Well, we iterate through the candidate list again:

for i in range(len(board)):
    for j in range(len(board[0])):
        cand = candidates[i][j]

And we retrieve all the sets from this cell’s region of interest:

        full_cand_row = self.get_row(i, candidates)
        full_cand_col = self.get_col(j, candidates)
        full_cand_box = self.get_box(j//3,i//3,candidates)

But there’s an issue. Each of these sets contain cand, so we need to remove cand from each set:

        # remove the current cell from each section
        cand_row = full_cand_row[:j] + full_cand_row[j+1:]
        cand_col = full_cand_col[:i] + full_cand_col[i+1:]
        box_idx = 3*(j//3)+i//3
        cand_box = full_cand_box[:box_idx] + full_cand_box[box_idx+1:]

Now we iterate through the elements of cand, checking its row/col/box in hopes that this specific element only occurs once. As stated above, we only need 1 of 4 conditions to be true in order to set the cell to n.

    for n in cand:
        # look at entire row/col/box to see if n is in there
        row_flag = True
        col_flag = True
        box_flag = True
    for s in cand_row:
        if n in s:
            row_flag = False
            break
    for s in cand_col:
        if n in s:
            col_flag = False
            break
    for s in cand_box:
        if n in s:
            box_flag = False
            break

Then if any of these conditions are true (or cand only has 1 element), we can populate the board with our number.

    if row_flag or col_flag or box_flag or len(cand) == 1:
        board[i][j] = str(n)
        candidates[i][j] = set([-1])
        placed_flag = True
        break

After every placement, we must regenerate our entire list of candidates. The regions of influence have changed due to this placement, so certain candidates are no longer valid. placed_flag operates as an early-restart for the program. I could optimize this to only refresh the candidates in the row/col/box, but it works well enough without that.

So…that’s it right? We just keep looping through and regenerating these candidates, and by process of elimination, we eventually find the solution?

Nope. There’s one more important caveat, and it’s what makes Sudoku hard for a human to solve.

Step 3: Bifurcations, or Guessing

While valid Sudoku problems will always have a unique solution (though I have yet to prove it), simple Sudoku problems don’t require any guessing. And on Leetcode, the first test passes at this point – it’s a verification that your basic solving works.

But the more difficult problems require a guess. You get to a point where there is no way forward unless you try. This area is where I struggle wtih Sudoku a lot and generally kind of hate playing the game. If you’re solving with pencil and paper, you get caught in a string of guesses, so when one guess ends up being wrong it’s unclear which guesses were valid or not and which ones were based on old guesses, and eventually your paper ends up totally messed up and smudged.

The formal name for guessing in Sudoku is “Bifurcation”, which means “the division of something into two branches or parts”. If we can limit ourselves to a binary guess, then we can try both routes and backtrack if we end up with an error.

Anyways, a computer which has perfect memory (well unless we overflow it) is very well-suited for the task.

Once again, we iterate through our candidates:

for i in range(len(board)):
   for j in range(len(board[0])):
       cand = candidates[i][j]

If -1 is in cand then it is invalid, and if candidate has more than 2 elements then we skip it. Technically we don’t need to skip it (and I suspect that more complex puzzles might even require a 3-way guess), but putting this exit in now saves time and still lets us pass the tests on Leetcode.

       if -1 in cand or len(cand) > 2:
           continue

Otherwise, we iterate through the numbers in cand and “test” them by inserting them into our board.

        for num in cand:
            copy = self.boardDeepCopy(board)
            copy[i][j] = str(num)

We insert the number into a deep copy of our current board, and then send this board recursively into our solve function. This recursive function might have subsequent guesses too!

            res, board_out = self.solveSudoku(copy)

If the board is solved, we return (True, board). We then copy the resulting board back into our original board. Otherwise, we get a False if the solver encounters an invalid situation. This occurs when len(cand) == 0 at any point. This means no possible digit can be in this cell, which violates the rules of Sudoku.

            if res:
                self.boardDeepCopyTo(board_out, board)
                return (True, board)

And that’s the solution! Well, minus a big while loop and some flags. The Leetcode asks for the board to be modified in-place so technically the returns are not used by the grading software, we just use it for convenince.

The full code can be found on Github here.

Addendum: Improving my code

I can definitely improve this a lot, and that may be a project for the future – my brother suggested using a Linked List to represent the board state, and a tree to represent different guesses. That would be a lot more space-efficient than what I’m doing right now, which is copying the entire board over and over again.

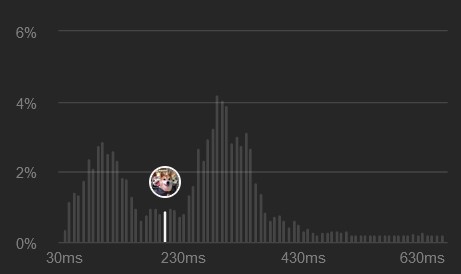
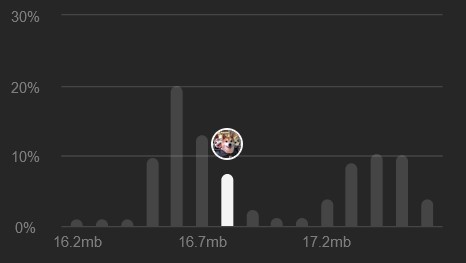
Leetcode also shows that I’m not exactly top-notch in time/space here either, I’m sort of middle-of-the-pack.

Time:

asdf

Memory:

asdf

But I’m still happy with what I’ve got done here – I pleasantly surprised myself by creating this solver.

If you got this far, thank you for reading my blog post! I’d love to hear your thoughts, so please reach out at my email shown at the bottom of the website. Thanks!